Bangun Ruang Sisi Lengkung Bagian 1 - Tabung

TABUNG

1. Unsur-unsur tabung

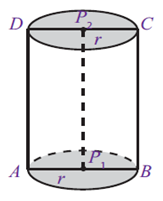
Amatilah gambar tabung di samping. Unsur – unsur tabung dapat diuraikan sebagai berikut:

a.       Jari – jari tabung (r), yaitu garis AP₁ = P₁B = DP₂ = P₂C

b.      Diameter (d), yaitu garis AB = CD

c.       Pusat lingkaran, yaitu titik P₁ dan P₂

d.      Sisi alas tabung (atas dan bawah yang diarsir), yaitu lingkaran P₁ dan P₂

e.       Tinggi tabung (t), yaitu garis yang menghubungkan P₁ dan P₂

f.       Selimut tabung, yaitu sisi lengkung tabung

 

2.      Luas Permukaan Tabung

a.     Luas Selimut Tabung

Luas selimut tabung adalah luas sisi lengkung tabung tanpa tutup(alas) atas dan tutup bawah.

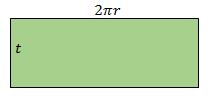
Perhatikan gamnbar di bawah ini!

Jika tabung tanpa tutup, kemudian di potong akan terbentuk menjadi sebuah persegi panjang,

panjangnya = keliling lingkaran, dan

lebarnya = tinggi lingkaran,

maka dapat dibuat kesimpulan bahwa:

Luas selimut tabung  = Luas Persegipanjang

                                   = p x l

                                   = 2πr x t

Luas selimut Tabung =  2πrt

Jadi, Luas selimut tabung: Lst = 2πrt

b. Luas Permukaan Tabung

Luas permukaan tabung merupakan luas seluruh tabung yang terdiri dari luas sisi lengkung(selimut tabung) dan luas tutup atas dan tutup bawah (lingkaran)

Luas permukaan tabung   = Luas tutup atas + luas selimut + luas tutup bawah

                                         = πr² + 2πrt + πr²

                                          = 2πr² + 2πrt

                                         = 2πr (r + t )

Jadi,  Luas tabung = 2πr (r + t 

3.      Volume Tabung

Cara menentukan volume prisma sama seperti menentukan volume  prisma, yaitu:

Volume tabung  = Luas alas x tinggi

                       = luas lingkaran x  tinggi tabung

                       = πr² x t

                       = πr²t

Jadi , Volume tabung:Vt = πr²t

Dalam hal ini,

Vt = Volume tabung

π = 3, 14 atau π = 22/7

r= jari jari alas tabung

t = tinggi tabung

 

 

contoh soal:

1.      Sebuah tabung panjang jari – jarinya 7 cm dan tingginya 20cm, tentukan:

a.       Panjang diameter alasnya

b.      Luas selimut tabung

c.       Luas permukaan tabung

d.      Volume tabung

2.      Diketahui sebuah tabung jari-jarinya 7 cm, dan volume tabung 3.080 cm³, tentukan

a.       Tinggi tabung

b.      Luas selimut tabung

 

            Penyelesaian:

1.    Diketahui:

Jari – jari = r = 7 cm

Tinggi = t = 20 cm,  π = 

Ditanya:   a. Panjang diameter alas(d)

                 b. Luas selimut tabung (Lst)

                 c. Luas permukaan tabung (Lt)

                 d. Volume tabung (Vt)

jawab:

a.         Panjang diameter alas (d)

r =  

d = 2.r = 2 x 7cm = 14 cm

b.        Luas selimut tabung (lst)

        Lst = 2πrt

              = 2 x (22/7) x 7 x 20

              = 2 x 22  x 20

       Lst  = 880

       Jadi Luas selimut tabung = Lst = 880 cm²

c.         Luas permukaan tabung (Lt)

       Lt   = 2πr (r + t )

              = 2 x (22/7) x 7 x ( 7 + 20)

              =2 x 22 x (27)

         = 169,71

         =1.188

Jadi Luas permukaan tabung (Lt) = 1.188 cm²

d.      Volume tabung (Vt)

   Vt  = πr²t

         = 22/7 x 7 x 7 x 20

         = 22 x 7 20

         =3.080

Jadi Volume tabung (Vt)= 3.080 cm³

 

2.      Diketahui:

Jari – jari (r) = 7 cm

Volume tabung (Vt) = 3.080 cm³

π =  22/7

di tanya:      a. Tinggi tabung (t)

                    b.  Luas selimut tabung (Lst)

 jawab:

a.       Tinggi Tabung (t)

     Vt    = πr²t

3.080    = 22/7 x 7 x 7 x t

             = 22 x 7 x t

             = 154 x t

154x t   = 3.080

          t  = 3.080/154 = 20

jadi tinggi tabung(t) = 20 cm

 

b.      Luas selimut tabung (Lst)

  Lst = 2πrt

         = 2 x 22/7 x 7 x 20

         = 2 x 22  x 20

   Lst = 880

            Jadi Luas selimut tabung = Lst = 880 cm²

     Latihan soal 4.1           

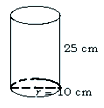
1.      Diketahui sebuah tabung jari-jarinya 10 cm, jika tinggi tabung 25 cm, hitunglah:

a.       Diameter tabung

b.      Luas selimut tabung

c.       Luas pernukaan tabung

d.      Volume abung

2.    Sebuah tabung luas selimutnya 352 cm² dan tinggi tabung 14 cm.  Hitunglah panjang jari jari tabung?

3.     
Gambar disamping menunjukan sebuah tabung tanpa tutup.

    

Hitunglah luas sisi dan volume tabung tersebut !

 

4. Sebuah pipa besi dengan jari jari 4 cm dan panjangny 5 m. permukaan selimutnya akan dicat. Hitunglah biaya pengecatan yang harus dikeluarkan jika biaya pengecatan adalah Rp 1.400,- per m².

5. Sebuah kaleng berbentuk balok dengan alas persegi memiliki panjang sisi 40 cm dan tingginya 50 cm. kaleng tersebut akan di isi oli, berapa banyak kaleng berbentuk tabung dengan diameter 5 cm dan tinggi 8 cm yang diperlukan untuk mengisi oli kedalam kaleng berbentuk balok tersebut?

 

Share this post