Materi Transformasi kelas 9 SMP
TRANSFORMASI
Refleksi (Pencerminan)
1. Pencerminan terhadap sebuah garis
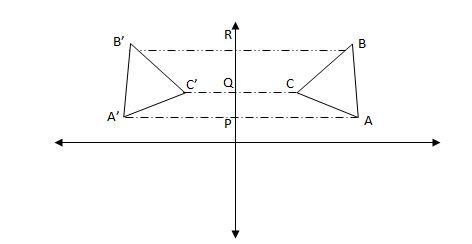
Perhatikan gambar di bawah ini
 |
| Materi Transformasi kelas 9 SMP |
Sifat-sifat pencerminan:
a. Jarak setiap titik asal terhadap cermin
sama dengan jarak bayangan terhadap cermin itu sendiri (AP=A’P, BR = B’R, CQ
=C’Q
b. Garis yang menghubungkan titik asal selalu
tegak lurus terhadap cermin
c. Pada pencerminan terhadap garis, maka suatu
bangun dengan bayanganya akan kongruen (Segitiga ABC = Segitiga A’B’C’)
2. Pencerminan terhadap garis pada bidang
koordinat
|
Titik Asal |
Refleksi
terhadap |
Bayangan |
|
(a, b) |
Sumbu x |
(a, - b) |
|
(a, b) |
Sumbu y |
(-a, b) |
|
(a, b) |
Garis y =
x |
(b, a) |
|
(a, b) |
Garis y =
-x |
(-b , -a) |
|
(a, b) |
Garis x =
m |
(2.m – a, b) |
|
(a, b) |
Garis y =
n |
(a, 2.n –
b ) |
Contoh soal:
Sebuah ttik dengan koordinat A ( 3, 4). Tentukan bayangan hasil
pencermina terhadap garis x = 2 !
Jawab
A = 3, b = 4, dan m= 2
Maka A’ (2.m – a, b)
A’ (2. 2 – 3, 4)
A’ (4 – 3, 4)
A’ (1, 4)
Jadi bayangan dari A (3, 4) adalah A’(1, 4)
Translasi (Pergeseran)
Dalam translasi, sebuah bangun berpindah
dengan arah dan jarak tertentu. Arah perpindahan disebut Arah Translasi dan
jarak perpindahan disebut besar translasi.
Jadi sebuah translasi di tentukan oleh arah
dan besarnya.
Pada translasi AB menyatakan besar dan arah
A ke B
Sedangkan AB hanya menyatakan jarak atau
panjang AB
Sehingga AB + BC = AC
+ artinya
“dilanjutkan dengan” tetapi AB + BC >AC
Pada translasi berlaku rumus
A(
a, b) ----------à (x, y), maka A’ (a + x, b+y)
Contoh soal
Tentukan koordinat bayangan titik A (2, 3)
pada trasnlasi (4, 5).
Jawab:
A = 2, b = 3, x = 4, y = 5
A(a, b) di translasikan oleh (4, 5) --à A’ (a + x, b + y)
àA’( 2+ 4, 3 + 5)
è A’ (6, 8)
Rotasi (Perputaran)
Rotasi pada bidang datar ditentukan oleh
pusat rotasi, besar sudut rotasi dan arah rotasi ( searah jarum jam atau
berlawanan arah jarum jam)
Pada rotasi dengan pusat O (0,0) sejauh 900
berlawanan arah jarum jam dapat di tulis
dengan O(0, 900)
Pada rotasi dengan pusat O (0,0) sejauh 900
searah arah jarum jam dapat di tulis
dengan O(0, 900)
Kesimpulan:
1. Arah rotasi yang berlawanan dengan arah
putaran jarum jam rotasinya bernilai positif (+)
2. Arah rotasi yang searah dengan arah putaran
jarum jam rotasinya bernilai negative (-)
Rumus rotasi
|
Titik asal |
Rotasi |
Bayangan |
|
(a, b) |
(0, 900) atau (0, -2700) |
(-b,a) |
|
(a, b) |
(0, -900) atau (0, 2700) |
(b, -a) |
|
(a, b) |
(0,1800) atau (0, -1800) |
(-a, -b) |
Contoh soal
Tentukan besar rotasi koordinat bayangan
dari titik B (-5, 4) pada rotasi dengan pusat O(0,0) sejauh 900 berlawanan arah jarum jam.
Jawab:
A
(-5, 4) (0,900)
A’ (-b, a)
Maka:
A (-5, 4) (0,900) A’ (-4, 5)
Latihan dan pembahasan
Titik A(-2, 5) ditranslasikan oleh {-4, -3}, kemudian dirotasikan dengan pusat O
sejau 900 berlawanan dengan arah jarum jam. Koornita baying titik tersebut
adalah ….
a. (-2, 6)
b. (-2, -6)
c. (2, 6)
d. (2, -6)
Pembahasan:
A(-2, 5) ditranslaskan
oleh {-4, -3}, maka bayangannya:
A’ (-2 + (-4), 5 + (-3))
A’ (-2 – 4, 5 – 3)
A’ (-6, 2)
Kemudian dirotasi dengan pusat O sejauh 900 berlawana arah
jarum jam
A (a, b) (0,900) A’ (-b, a)
A (-6, 2) (0,900)-----à A’ (-2,
-6)
Kunci Jawaban: B
Dilatasi (perkalian dg factor)
Dilatasi adalah transformasi bidang yang
memetakan seiap titik P pada bidang ke
satu titik P’ sedemikian sehingga OP’ = k. OP dengan O sebagai pusat dan k factor
skala.
OP’ = k. OP artinya OP’ adalah k kali OP
Rumus dilatasi
Pada dilatasi [O, k], maka:
A(a, b) ---------------à A’ (k x a, k x b)
Contoh:
Tentukan koordinat
bayangan titik B (-7, 6) pada dilatasi dengan pusat O (0,0) dan Faktor sekala
-4.
Jawab:
a = -7, b =
6 dan k = -4
B(a, b)
---------------à B’ (k x a, k x b)
B(-7, 6)
---------------à B’ (-4 x -7, -4 x 6)
B’ (28, -24)
Latihan sola dan pembahasan
Titik P (6, 8) diidlatasi dengan pusat
O(0,0) dan factor Skala 2, kemudian bayanganya di trasnlasikan dengan [-10,
12). Kordinat bayangan titik P adalah ….
Pembahasan
A=6, b=8,
dan k = 2
P(a, b)
---------------à P’ (k x a, k x b)
P(6, 8)
---------------à P’ (3 x 6, 3 x 8)
P’(18, 24)
kemudian ditransalsikan [-10, 12)
P’’ (18
+(-10), 24+12)
P’’(18-10,
24 + 12)
P’’(8, 36)
Jadi kordinat
bayangan P adalah (8, 36)

0 Response to "Materi Transformasi kelas 9 SMP"
Post a Comment